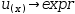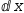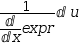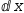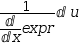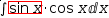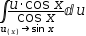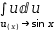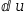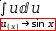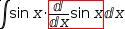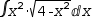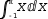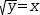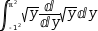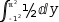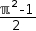3.4.1 U-Substitution
U-substitution is a calculus technique for integration.
It performs three different transformations, depending on the
context of the subject.
- If the subject is a subexpression of an integrand,
U-substitution uses the subexpression to synthesize a function.
- If the subject is the decoration on an integral that is the
result of a previous u-substitution, an inverse transformation is
performed, recovering the original integral.
- If the subject is an integrator, other expressions on the
display are harvested for a function definition to replace
subexpressions in the integrand. This form of u-substitution
is called integrator substitution.
The three transformations are described here.
Section
§4.4.2
contains more detailed explanations along with examples.
3.4.1.1 Synthesized U-substitution
The usual calculus technique of u-substitution is employed by selecting a
subexpression of the integrand and applying U-Substitution .
The subexpression becomes the right side of a
synthesized replacement function, depicted here by
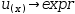 u(x)→expr. The integrand is rewritten by replacing the integrator
u(x)→expr. The integrand is rewritten by replacing the integrator 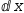 ⅆx:1 by
ⅆx:1 by
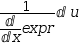 1÷ⅆexprⅆx⋅ⅆu:1, which can be seen to be the isolation of
1÷ⅆexprⅆx⋅ⅆu:1, which can be seen to be the isolation of 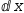 ⅆx:1 in the identity
ⅆx:1 in the identity
 ⅆuⅆx=ⅆexprⅆx. The synthesized function is added as a decoration to the integral.
ⅆuⅆx=ⅆexprⅆx. The synthesized function is added as a decoration to the integral.
The next step is to simplify the derivative introduced by
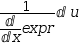 1÷ⅆexprⅆx⋅ⅆu:1. Because this next step is inevitable, it is performed
automatically by the u-substitution transformation.
1÷ⅆexprⅆx⋅ⅆu:1. Because this next step is inevitable, it is performed
automatically by the u-substitution transformation.
For example, applied to a subexpression of the integrand in
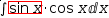 ∫.{sin x}⋅cos x ⅆx, U-Substitution transforms the integral into
∫.{sin x}⋅cos x ⅆx, U-Substitution transforms the integral into
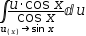 ∫u⋅cos x÷cos x ⅆ(u(x)→sin x). Simplification yields
∫u⋅cos x÷cos x ⅆ(u(x)→sin x). Simplification yields
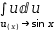 ∫u ⅆ(u(x)→sin x), which is more easily integrated.
∫u ⅆ(u(x)→sin x), which is more easily integrated.
3.4.1.2 Inverse U-substitution
Sometimes it is necessary to work backwards from an expression that contains an
integral with a decoration. Applied to a decoration, U-substitution performs an inverse operation, replacing all occurrences of the u
expression with the right side of the definition. The integrator is
augmented by an isolation of 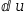 ⅆu:1 in the identity
ⅆu:1 in the identity
 ⅆuⅆx=ⅆexprⅆx.
ⅆuⅆx=ⅆexprⅆx.
For example, with the decoration in
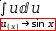 ∫u ⅆ.{u(x)→sin x}
selected, U-substitution produces
∫u ⅆ.{u(x)→sin x}
selected, U-substitution produces
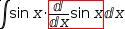 ∫sin x⋅.{ⅆsin xⅆx} ⅆx
∫sin x⋅.{ⅆsin xⅆx} ⅆx
which simplifies to
 ∫sin x⋅cos x ⅆx
∫sin x⋅cos x ⅆx.
3.4.1.3 Integrator Substitution
Integrator substitution is used when the substituted expression is not a
subexpression of the integrand. Applied when the integrator is the subject, U-substitution harvests a candidate equation from the other expressions in the
workspace. A successful candidate is supplied by any equation with the
integrator on one side and a substitution expression involving a
single variable on the other. The integrand is transformed by
replacing all occurrences of the integrator with the substitution
expression and replacing the integrator by the left side. Finally, the
integrand is augmented with the derivative of the function.
For example, consider u-substitution on the integrator of
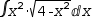 ∫x^2⋅√(4-x^2) ⅆx
in the presence of a candidate equation
∫x^2⋅√(4-x^2) ⅆx
in the presence of a candidate equation
 x=2⋅sin t. All occurrences of x will be replaced by
sin t, as will the integrator. The augment is
x=2⋅sin t. All occurrences of x will be replaced by
sin t, as will the integrator. The augment is
 x=2⋅sin t. The result is
x=2⋅sin t. The result is
 ∫(2⋅sin t)^2⋅√(4-(2⋅sin t)^2)⋅ⅆ2⋅sin tⅆt ⅆt.
∫(2⋅sin t)^2⋅√(4-(2⋅sin t)^2)⋅ⅆ2⋅sin tⅆt ⅆt.
If the integral has bounds, the single variable in the candidate
equation is isolated to obtain a mapping expression in terms of the
original integrator. The bounds are transformed by applying the
mapping expression.
To see how this works, consider the simple integral
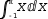 ∫-1, ℼ, x ⅆx
and the equation
∫-1, ℼ, x ⅆx
and the equation
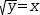 √y=x. Integrator substitution produces
√y=x. Integrator substitution produces
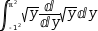 ∫-1^2, ℼ^2, √y⋅ⅆ√yⅆy ⅆy. Simplification produces
∫-1^2, ℼ^2, √y⋅ⅆ√yⅆy ⅆy. Simplification produces
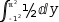 ∫-1^2, ℼ^2, 1/2 ⅆy. Simplification and evaluation produces the final result
∫-1^2, ℼ^2, 1/2 ⅆy. Simplification and evaluation produces the final result
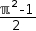 (ℼ^2-1)÷2. The original integral simplified directly produces the same result.
(ℼ^2-1)÷2. The original integral simplified directly produces the same result.